Video Transcript: "The Determinants of Cardiac Output"
(also available here in PDF format for download and printing)
An understanding of the determinants of cardiac output is essential to both medical specialists in their dealing with heart disease and hypertension, and to surgical specialists who deal with shock states and the maintenance of adequate circulation during surgical procedures. In this program, I'll introduce you to some fundamental yet often misunderstood concepts about the determinants of cardiac output by examining this hydraulic model of the cardiovascular system.
A model gives us a unique opportunity to directly observe phenomena that we can measure only indirectly in the human body. Any model is as potentially useful as its ability to replicate the body's response to identical stimuli. As you will see during the program, this model will mimic physiologic responses very well because of a special component: The pump.
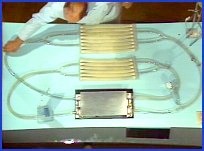
The pump is a homologue of the heart. Each of the two pumps has a ventricle, an inlet and an outlet valve, and an atrium. The left pump is connected to a simulated aorta, through which fluid flows to systemic arterioles and a distensible capillary bed, which empties into venules, a vena cava, and back to the right heart pump. The pulmonary circuit has a pulmonary artery, arterioles, a compliant capillary bed, emptying into simulated venioles and pulmonary veins, back to the left pump. At this point, the systemic and pulmonary circuits cross, making this system a single circuit with the two pumps in series, just like in the human cardiovascular system.
As previously stated, the most significant characteristic of the model -- and the one that allows it to reproduce cardiovascular phenomena -- is the pump. These pumps, unlike most, do not suck at their inlets to fill. Let's compare this non-sucking pump to one that does suck to fill.

This is a standard roller pump commonly used in cardiopulmonary bypass. The rollers compress the tubing to push fluid forward. The tubing recoils to its original shape behind the roller, thereby generating suction that refills the tubing with fluid. Since the tubing is always full because of the suction, the output is determined by the speed of the pump. Pump output is therefore equal to stroke rate times stroke volume -- that is, the speed of the pump times the volume of the fluid between the rollers. This pump therefore not only moves the fluid but determines the flow rate by virtue of pump speed. External or systemic factors, such as increase in hydrostatic pressure generated by lifting the fluid container above the level of the pump, do not alter the pump output.

In contrast, this non-sucking pump has a ventricle that is normally flat instead of round on cross-section. After this ventricle is compressed, it does not rebound and suck as in the other pump. It fills passively after being emptied. If I turn the pump on at a rate of 80 beats per minute, you can see that there is no flow. Even if I increase the rate above 80 beats a minute, and increase the strength of the driving force of the impellers by hand-cranking the pump, there is no output. The pressure in the system is below pump level. Since the pump cannot suck to fill, no fluid runs into the ventricles, so there can be no output. It is only when the bottle is raised above pump level that flow occurs. Therefore, flow in a non-sucking pump is controlled by the amount of pressure in the system. Increasing the pressure increases the flow. Decreasing the pressure decreases the flow.
So the output of a sucking pump is controlled by pump factors, whereas the output of a non-sucking pump is controlled by systemic factors. Now let's go back to the model and see what this non-sucking pump does in that system.
With ventricular capacity of 100 CCs, these pumps are capable of pumping 8 liters a minute at the current rate of 80 beats a minute, yet no circulation is occurring. Increasing the pump rate and strength of contraction by hand-cranking also effects no flow. But remember, we just observed that non-sucking pumps cannot pump without there being pressure in the system. You can see that the compliant beds are flaccid, so perhaps there is insufficient pressure in the system. A U-tube connected to the arteries allows me to confirm that the pressure in the system is below pump level -- this black line being equal to the pump level, and the green fluid equal to the system pressure. The pressure is low because of the low volume of fluid in the system. The model is in hypovolemic shock. Just as in the human with inadequate pressure in the cardiovascular system from low fluid volume, increasing the heart rate or strength of contraction does not improve cardiac output.
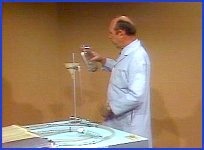
I can increase the fluid volume in this system through this intravascular line. I'll add 250 CCs of fluid and see if that's enough to promote flow. As you can see, this amount of fluid did not increase the flow. And correspondingly, that amount of fluid did not fill this flaccid system to a level above the pump level. Therefore, if that was an inadequate amount, we'll add 250 CCs more and see if that will start the flow. That did cause some flow. So we now have one-and-a-half liters a minute flow. Correspondingly, the pressure within the system is now above pump level. If a small amount of fluid caused that amount of flow, let's see what an additional 250 CCs will do. This additional 250 CCs caused a marked difference in flow -- as you can see, we now have four liters a minute. With this increased flow, we also observe that the pressure in the system is now much higher than it was before. We have now seen a significant increase in flow.
So what we have seen is that increase in fluid volume in the vascular system increases the output. Although the increase was not linear, since the 250 CCs I put in last changed the flow rate much more than the 500 CCs that was put in during the first two transfusions.
So we know that one factor that determines pressure in the system -- and thus determines flow -- is fluid volume. The pressure in any hydraulic system is a product of volume and system compliance. So let's look at the compliance of this system.
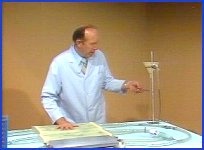
Compliance of the beds can be decreased by contracting the muscles around the beds, thereby decreasing distensibility. If you will notice, look at the manometer and see as I press on the beds how the pressure increases.
I'll turn on the pump now and see if this increase in pressure does increase the flow. As I press on the beds, you can see the increase in flow on the flow meter. A corollary in human physiology is seen when vasopressors increase cardiac output by decreasing vascular compliance, and when spinal anesthesia and vasorelaxers decrease cardiac output by increasing vascular compliance.
So one determinant of output that we have observed thus far is the pressure in the vascular system that forces fluid into the non-sucking heart and which has two components -- the fluid in the system and compliance. This pressure, which is the result of blood volume and vascular compliance, is called mean vascular pressure, and was first described by Weber in 1863.
"Mean vascular pressure" is perhaps an unfamiliar term to you. The mean vascular pressure is the pressure in the vascular system with the heart stopped, after pressures have equilibrated between the arteries, capillaries, and veins. Mean vascular pressure is normally between 16 and 18 millimeters of mercury above mid-heart level, but has been measured up to 20 to 30 millimeters in high output states, and as low as 6 to 8 millimeters of mercury in shock states. Yet we can again confirm that with a pressure sufficient to cause flow, an increase in rate and strength of contraction does not increase the output. A corollary in human physiology is seen when digitalis or an increase in pacemaker rate may not change cardiac output when there is no myocardial energy failure. I'll come back to this concept of energy failure in a few minutes.
So we have determined a factor that can cause flow to increase.

However, there may be other factors that can reduce flow, even in the presence of a positive mean vascular pressure. The most obvious candidate is resistance. Certainly a tube clamp placed partially across a vessel will add considerable resistance to flow. Let's see what effect such resistance does have on pump output.
Without the resistance, the pressure on the arterial side is very low -- being 80 over 20. The flow rate is now four-and-one-half liters per minute. Now let's see what adding a significant resistance will do. The pressure is now 220 over 100 -- certainly a significant resistance. Yet the flow remains four-and-a-half liters per minute. The pump is strong enough to just force the fluid right on by the resistance point. So the flow stays at four liters a minute, unchanged. Clinically, we see a similar phenomenon with aortic stenosis, arteriolar hypertension, and coarctation of the aorta. People with such problems still have normal cardiac output as long as their heart is strong enough to eject its contents.

But let's see what happens if we add a similar resistance to the inlet of the pump. Obviously a dramatic decrease in output.
But why does the resistance at the inlet of the pump slow pump output, while it has no effect at the outlet of the pump? The difference between the two is the relative amount of compliant bed upstream from the two resistance points. In the case of outlet resistance, there is very little distensible bed between the resistance point and the pump. But with inlet resistance, there is a large compliant bed upstream. The compliant bed stores potential energy from the pump ejection that would otherwise be in the form of kinetic energy. But with outlet resistance, there is only minimal stored potential energy because there is very little distensible bed upstream. Therefore there is much more kinetic energy available to force the fluid past the resistance.
Total vascular resistance therefore is not a parameter that is a factor in determining cardiac output. It is instead the combination of a resistance point and the vascular distensibility upstream from that resistance point that together impede the flow to the pump inlet and decrease pump output. "Inlet impedance" is the term we will use to describe this combination of resistance and compliance that can decrease cardiac output. Take note that again I am using a term that you may not be accustomed to using in this context.

The most significant factor in minimizing inlet impedance to a non-sucking pump is the atrium. As I turn on the pump, you will notice that the pump's output it pulsatile, while inflow to the pump is non-pulsatile. If I momentarily stop the atrium from working, you can see that the venous flow becomes pulsatile, and the flow decreases significantly. By being empty and distensible, when the inlet valve closes, the atrium allows uninterrupted venous flow to the pump during ventricular systole. While during diastole venous and atrial flow move into the ventricle unimpeded. Although atrial displacement constitutes only 15% of the volume ejected by the ventricle at each beat, the atrial effect makes possible four times the flow that would occur without some mechanism to prevent the inertia of starting and stopping flow to the intermittent pump.
Atria, therefore, significantly minimize the inlet impedance to the pumps. Clinical corollaries of an increased inlet impedance that reduces cardiac output include mitral stenosis, venous obstruction, atrial fibrillation, nodal rhythm, cardiac tamponnade, ventricular non-compliance, and extremely rapid heart rate. Clinical corollaries of reduced inlet impedance with concomitant increase in cardiac output include arterial-venous fistula that bypasses the compliant bed, and exercise, which uses muscle-vein pumps to force fluid past inlet resistance points.
So far, we have seen two determinants of cardiac output: Mean vascular pressure, which has as its components fluid volume and system compliance; and inlet impedance, which is a combination of resistance with a distensible bed upstream from that resistance. We also confirmed that neither an increase in rate nor strength of contraction increase the flow when I hand-crank the pump.
But obviously rate is determining output now, since the pump is stopped. At what point do increases in rate no longer cause increases in output? To answer that question, you must first understand that until this point we've been examining conditions where the pump is exerting excess energy above what was used for circulation. In other words, an increase in mean vascular pressure increased fluid flow into the ventricles, which increased cardiac output. But if a ventricle has already filled completely, an increase in mean vascular pressure obviously could not increase cardiac output, since the ventricle could not hold any more fluid. Therefore, we must make a distinction between these two conditions.
"Pump energy excess," another new concept, is that state where the pump is expending more energy than needed to eject the fluid from the ventricles. It is this state that we've been examining so far, in which we found the determinants of pump output to be mean vascular pressure and inlet impedance. We know that human hearts in normal, day-to-day living expend excess energy because propranalol, which in therapeutic dosage reduces heart rate and strength of myocardial contraction, causes no decrease in output unless the ventricles are in energy failure.
"Pump energy failure," not to be confused with the term "congestive heart failure," is that state where the pump is not expending sufficient energy to prevent the ventricles from filling completely before the end of diastole.
Now let's examine the determinants of cardiac output during myocardial energy failure.
I think we can already agree on one: Rate. Right now the pump is in energy failure because of low -- or in this case, zero -- rate. If I increase the rate to one beat per minute, the maximal ventricular volume of 100 CCs is ejected, and we have a flow of 100 CCs per minute. At two beats per minute, 200 CCs is ejected, and so on until the pump is going fast enough that the ventricles no longer have time to fill completely at this particular mean vascular pressure and inlet impedance. The pump is then back in energy excess.
Clinically, we see pump energy failure in complete heart block at a rate of 20 to 30 beats a minute. If we increase the heart rate, there are concomitant increases in cardiac output until about 70 beats a minute, at which time the heart is no longer in power failure. Then, further increases in pacemaker rate cause no further increase in cardiac output.
So one determinant of cardiac output during myocardial energy failure is rate. The other myocardial energy failure state which, we are about to examine, is when the strength of contraction is insufficient to overcome an outlet impedance.

Remember our earlier example, where a strongly working pump was able to overcome an outlet impedance. But if the strength of contraction were insufficient, which is a condition I can simulate by manually contracting the ventricles, there will be a significant decrease in flow. The outflow impedance, together with the insufficient strength of contraction, limits the emptying of the ventricles. Therefore they fill completely before the end of diastole, thus causing intermittent inflow. This limited inflow reduces pump output. Clinical corollaries are seen in all myocardial energy failure states, such as myocarditis, myocardial infarction, and aortic outflow obstruction with weak ventricular contractions.

With the insight that we have gained from the model, you should be able to ascertain that Starling's Law -- which states that the greater the filling at diastole, the greater the strength of contraction at systole -- expresses a mechanism of cardiac output control only during myocardial energy failure. At all other times, it has only energy conservation implications.
You should also realize that Poiseuille's Law -- which expresses outlet resistance as a determinant of cardiac output -- is once again only valid during myocardial energy failure. At all other times, it merely expresses a pressure gradient across an outlet resistance point.
All available data from human physiologic experience correlates with the findings we have seen in the model. Therefore, I believe we are safe in presuming that the human heart is a non-sucking, intermittent outflow, continuous inflow pump. We can also presume from the model that cardiac output has two separate sets of determinants, only one of which can be operative at a time. It is the set that potentially limits the output most that is the determinant at any time.

The first set is applicable when the heart is in myocardial energy excess and includes mean vascular pressure -- which includes fluid volume and system compliance -- and inlet impedance -- which is the product of a resistance point and a distensible bed upstream from that resistance point.
The second set of determinants is applicable when the heart is in myocardial energy failure, and includes low rate and/or insufficient myocardial contraction to overcome outlet impedance.
You have now observed that most phenomena seen in the cardiovascular system need no other explanation than simple hydraulic mechanics.
("The Determinants of Cardiac Output" was produced by Biomedical Communications, University of Arizona Health Sciences Center. © The University of Arizona. All rights reserved. Used with permission.)